선형회귀란

머신러닝에서 가장 기본적이고 해석이 용이한 모델

• 목적: 수치형 데이터를 예측
• 특징
• 단순하고 직관적
• 해석이 용이하여 기초 학습에 적합
• 다른 모델들의 출발점이 되는 기초 모델

문제 개요

여행사가 고객에게 여행 보험 패키지를 제공하고 있으며, 구매 여부를 예측하는 모델을 만든다고 가정합니다.

• 입력 데이터: 나이, 고용유형, 구매여부 등 총 9개 변수
• 출력 데이터: 보험 패키지 구매 여부 (확률 or 이진 분류)
• 데이터 규모: 고객 1,987명
• 목표: 고객의 특성을 기반으로 구매 가능성을 예측

💡 예시: "나이, 연수입" → "AnnualIncome 예측" 또는 "여행보험 구매여부" → "구매 확률 예측"

선형회귀의 개념

독립변수(X)와 종속변수(Y) 간의 선형 관계를 찾아내는 모델

• 회귀(Regression): 연속형 변수 예측
• 분류(Classification): 범주형 변수 예측

예시:

• 회귀: 나이 → 연수입 예측
• 분류: 나이, 연수입 → 보험 가입 여부 예측

모델 수식과 계수 해석

회귀식:

$y = w_1x_1 + w_2x_2 + \cdots + b$

• y → 예측값 (종속변수)
• x → 입력값 (독립변수)
• w → 계수 (Coefficient, 영향력의 크기와 방향)
• b → 절편 (Intercept, 기준값)

데이터 준비와 전처리

데이터 전처리 관련 이전 블로그

import pandas as pd
 
data_file = "public/TravelInsurancePrediction.csv"
df = pd.read_csv(data_file)
 
# 불필요 컬럼/결측치 제거
data = df.drop(columns='Unnamed: 0').dropna()
data = data.drop(index=[1989])
display(data.shape), display(data.head())

단일 독립변수 선형회귀

from sklearn.linear_model import LinearRegression
 
x = data[['Age']]
y = data['AnnualIncome']
 
model = LinearRegression()
model.fit(x, y)
 
print(model.coef_, model.intercept_)
# [-2600.26], 1009861.25

회귀식:

$y = -2600.26 \times Age + 1009861.25$

다중 선형회귀

x = data[['Age', 'TravelInsurance']]
y = data['AnnualIncome']
 
model.fit(x, y)
print(model.coef_, model.intercept_)
# [-5755.55, 314075.47], 1009861.25

회귀식:

$y = -5755.55 \times Age + 314075.47 \times TravelInsurance + 1009861.25$

손실 함수와 최적화

손실 함수 (Loss Function)

모델의 예측값과 실제값 차이를 수치화한 값

• MAE (평균절대오차, Mean Absolute Error): 절대값 기준 오차
• MSE (평균제곱오차, Mean Squared Error): 제곱 기준 오차 → 큰 오차에 민감
• RMSE (Root Mean Squared Error): 제곱 평균 오차의 제곱근

from sklearn.metrics import mean_absolute_error, mean_squared_error
 
z_all = model.predict(x)
mae = mean_absolute_error(y, z_all)
mse = mean_squared_error(y, z_all)
rmse = mse**0.5

경사하강법 (Gradient Descent)

모델의 계수(w)와 절편(b)을 학습하는 방법

• 초기 임의의 값 설정
• 손실함수의 기울기(Gradient)를 계산
• 기울기 반대 방향으로 조금씩 이동하며 최적화
• 손실 함수가 최소화되는 지점에서 수렴

학습률(learning rate)이 크면 발산, 작으면 수렴 속도가 느림

범주형 변수 처리

from sklearn.preprocessing import LabelEncoder
 
le = LabelEncoder()
data['GraduateOrNot'] = le.fit_transform(data['GraduateOrNot'])

모델 평가 지표

R² (결정계수)

$R^2 = 1 - \frac{SSR}{SST}$

• SSR: 잔차 제곱합
• SST: 총 변동합
• 값이 1에 가까울수록 설명력이 높음

from sklearn.metrics import r2_score
 
r2 = r2_score(y, z_all)
print(r2)

시각화 & 해석

예측선과 실제 데이터 비교

import matplotlib.pyplot as plt
 
plt.scatter(data['Age'], data['AnnualIncome'], label="Actual")
plt.plot(data['Age'], z_all, color='red', label="Predicted")
plt.xlabel("Age")
plt.ylabel("AnnualIncome")
plt.legend()
plt.show()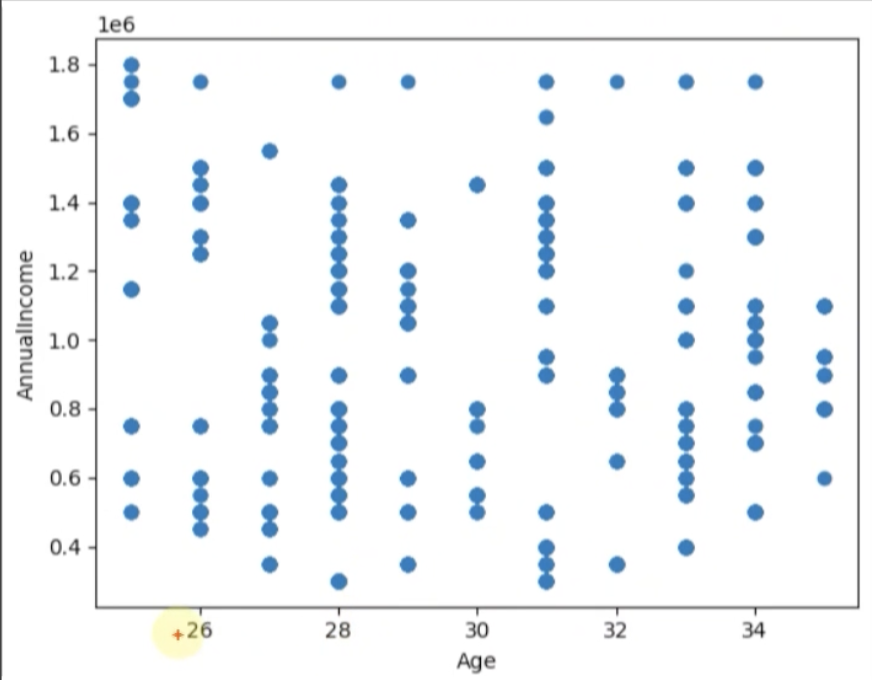

잔차 분석

잔차는 랜덤하게 분포해야 함 → 패턴이 있으면 모델이 적절하지 않음

res = y - z_all
plt.scatter(z_all, res)
plt.axhline(y=0, color="red", linestyle="--")
plt.xlabel("Predicted")
plt.ylabel("Residuals")
plt.show()

결론

• 선형회귀는 단순하지만 해석과 구현이 쉬워 데이터 분석 입문에 적합
• 손실 함수와 경사하강법을 통해 계수를 최적화
• 평가 지표(R², MAE, RMSE)로 모델 성능 검증
• 잔차 분석을 통해 모델 적합성 확인 가능