BlogBooksPlaylistDashboard

선형회귀 모델의 평가 및 과적합

2025-10-03

목표

  • 선형회귀 모델의 성능평가 지표를 이해하고 적용할 수 있다.
  • 과적합(Overfitting) 문제를 진단하고 해결하는 방법을 학습한다.
  • 일반화 성능을 높이는 데이터 분할 및 교차검증 방법을 익힌다.

선형회귀 모델 개요

선형회귀(Linear Regression) 모델은 입력 변수(X)와 출력 변수(y) 간의 선형 관계를 추정하는 가장 기본적인 회귀 알고리즘입니다.

  • 구조가 단순하여 해석이 용이하지만, 과적합(overfitting) 또는 과소적합(underfitting) 문제가 발생할 수 있습니다.
  • 따라서, 모델 성능을 올바르게 평가하고 일반화 능력을 확보하는 과정이 매우 중요합니다.

주요 평가 지표

🔗 회귀모델 평가지표의 개념 이전 블로그 보기

지표특징이상치에 대한 민감도
MAE (Mean Absolute Error)오차의 절댓값 평균이상치에 둔감
MSE (Mean Squared Error)오차의 제곱 평균이상치에 매우 민감
RMSE (Root Mean Squared Error)MSE의 제곱근실제 단위와 동일하여 해석 용이
R² (결정계수)모델이 데이터를 얼마나 잘 설명하는지(1에 가까울수록 좋음)-

✅ Tip

  • 이상치(outlier)가 많은 경우 → MAE 사용
  • 이상치가 적고 세밀한 차이를 보고 싶을 때 → MSE / RMSE 사용

데이터 준비와 전처리

🔗 데이터 전처리 관련 이전 블로그 보기

import pandas as pd
 
data_file = "public/TravelInsurancePrediction.csv"
df = pd.read_csv(data_file)
 
# 불필요 컬럼/결측치 제거
data = df.drop(columns='Unnamed: 0').dropna()
data = data.drop(index=[1989])
display(data.shape), display(data.head())

범주형 변수 인코딩

from sklearn.preprocessing import LabelEncoder
 
le_emp = LabelEncoder()
le_grad = LabelEncoder()
le_flyer = LabelEncoder()
le_travel = LabelEncoder()
 
df_processed = data.copy()
df_processed['Employment_Type_Encoded'] = le_emp.fit_transform(data['Employment Type'])
df_processed['GraduateOrNot_Encoded'] = le_grad.fit_transform(data['GraduateOrNot'])
df_processed['FrequentFlyer_Encoded'] = le_flyer.fit_transform(data['FrequentFlyer'])
df_processed['EverTravelledAbroad_Encoded'] = le_travel.fit_transform(data['EverTravelledAbroad'])

특성 변수와 목표 변수 분리

feature_columns = [
    'Age',
    'Employment_Type_Encoded',
    'GraduateOrNot_Encoded',
    'FamilyMembers',
    'ChronicDiseases',
    'FrequentFlyer_Encoded',
    'EverTravelledAbroad_Encoded',
    'TravelInsurance'
]
X = df_processed[feature_columns]
y = df_processed['AnnualIncome']

선형회귀 모델 학습

from sklearn.linear_model import LinearRegression
 
model = LinearRegression()
model.fit(X, y)
 
# 예측
y_pred = model.predict(X)

성능평가

from numpy import sqrt
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
 
mae = mean_absolute_error(y, y_pred)
mse = mean_squared_error(y, y_pred)
rmse = sqrt(mse)
r2 = r2_score(y, y_pred)
 
mae, mse, rmse, r2

잔차 분석 (Residual Analysis)

잔차(Residual) = 실제값 - 예측값
모델의 예측 오차를 의미하며, 패턴 없이 무작위로 분포하면 좋은 모델입니다.

res = y - y_pred
 
res.mean(), res.std(), res.max(), res.min()

시각화 1 - 예측값 vs 실제값

import matplotlib.pyplot as plt
 
plt.scatter(y_pred, y)
plt.xlabel("Predicted Values")
plt.ylabel("Actual Values")
plt.title("Predicted vs Actual")
plt.show()

시각화 2 - 잔차 분포 확인

plt.hist(res, bins=30)
plt.title("Residual Distribution")
plt.show()

해석 가이드

  • 잔차가 0 주변에 고르게 분포 → 좋은 모델
  • 특정 방향으로 치우치거나 곡선 패턴 → 비선형 관계 가능성
  • 정규분포 형태 → 선형회귀 가정 만족

데이터 분할 및 평가

훈련 데이터와 테스트 데이터를 분리하여 일반화 성능을 확인합니다.

from sklearn.model_selection import train_test_split
 
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)
 
model = LinearRegression()
model.fit(X_train, y_train)
 
y_test_pred = model.predict(X_test)
 
mae = mean_absolute_error(y_test, y_test_pred)
mse = mean_squared_error(y_test, y_test_pred)
 
print(mae, mse)

과적합(Overfitting) 개념

구분설명
과적합(Overfitting)학습데이터에 과도하게 적합되어, 새로운 데이터 예측력이 낮은 상태
과소적합(Underfitting)학습데이터조차 충분히 설명하지 못함

test_size 변화에 따른 성능 비교

from sklearn.metrics import mean_absolute_error
 
for x in [0.2, 0.3, 0.4, 0.5]:
  X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=x, random_state=42 )
 
  model = LinearRegression()
  model.fit(X_train, y_train)
 
  y_train_pred = model.predict(X_train) # 학습 데이터 예측값
  y_test_pred = model.predict(X_test) # 검증 데이터 예측값
 
  train_mae = mean_absolute_error(y_train, y_train_pred)
  test_mae = mean_absolute_error(y_test, y_test_pred)
 
  print(x, train_mae, test_mae)

과적합 방지 기법

  1. 교차검증(Cross Validation)

교차검증은 데이터를 여러 조각으로 나누어 모델을 반복 학습/검증함으로써 과적합을 방지합니다.

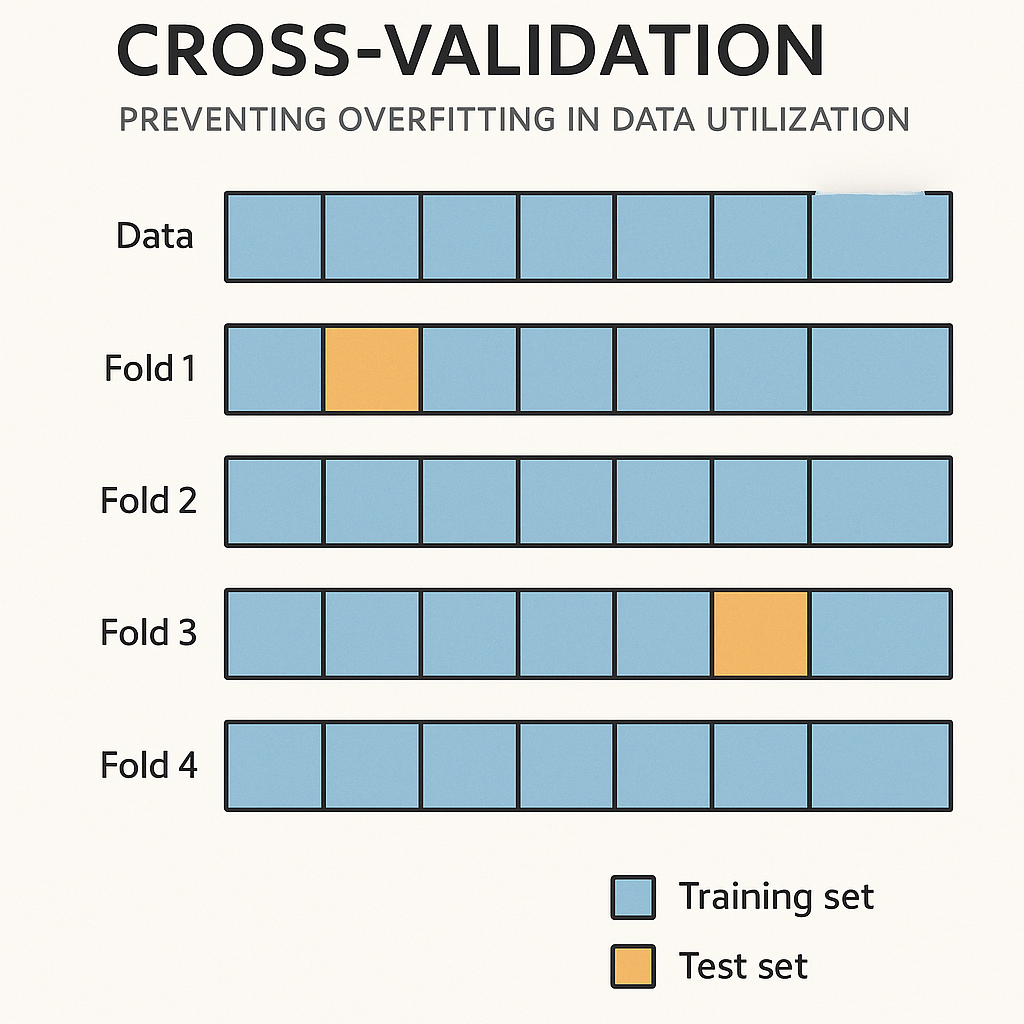
교차검증 개념도

from sklearn.model_selection import cross_val_score
 
scores = cross_val_score(model, X, y, cv=5, scoring='r2')
print("교차검증 R² 평균:", scores.mean())
  1. 정규화 회귀(L1, L2)

회귀계수에 제약(패널티)을 부여하여 과적합을 완화하는 기법입니다.

방법패널티효과
RidgeL2 규제큰 가중치를 부드럽게 줄임
LassoL1 규제중요하지 않은 특성의 계수를 0으로 만들어 변수 선택 기능 수행
from sklearn.linear_model import Ridge, Lasso
from sklearn.metrics import mean_absolute_error
 
# Ridge 예시
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
 
train_mae = mean_absolute_error(y_train, ridge.predict(X_train))
test_mae = mean_absolute_error(y_test, ridge.predict(X_test))
 
print("Ridge:", train_mae, test_mae)
 
# Lasso 예시
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)
 
train_mae = mean_absolute_error(y_train, lasso.predict(X_train))
test_mae = mean_absolute_error(y_test, lasso.predict(X_test))
 
print("Lasso:", train_mae, test_mae)

마무리 정리

구분주요 내용핵심 포인트
평가 지표MAE, MSE, RMSE, R²이상치 여부에 따라 지표를 선택
- 이상치 多 → MAE
- 이상치 少 → MSE / RMSE
잔차 분석예측 오차의 분포를 통해 모델 적합성 판단잔차가 무작위로 분포하고
정규분포 형태를 띠면 좋은 모델
데이터 분할훈련 데이터 / 테스트 데이터 분리모델의 일반화 성능 확보를 위한 핵심 과정
과적합 방지교차검증, 정규화 회귀 (Lasso / Ridge)가중치 제약으로 복잡도 조절
Lasso는 변수 선택 기능도 수행

💡 결론

단순히 학습 데이터를 잘 맞추는 모델이 아니라,
새로운 데이터에서도 일관된 성능을 내는 일반화 모델이 진정한 목표입니다.

  • 모델 평가 지표를 상황에 맞게 선택하고
  • 잔차 분석으로 모델의 구조적 문제를 파악하며
  • 데이터 분할 / 교차검증 / 정규화 기법으로 과적합을 방지한다면

➡️ 보다 안정적이고 신뢰할 수 있는 회귀 모델을 구축할 수 있습니다.

댓글

GitHub 계정으로 댓글을 남겨보세요!